14  ‘Throw’ verbs in Spanish: RepRoducing the results of a corpus linguistics study

About the author of this chapter

Poppy Siahaan [pɔpi siahaʔan] is a lecturer at the Institute of Languages and Cultures of the Islamicate World at the University of Cologne. She has a keen interest in semantics, particularly metaphors, and studies the connections between language, culture, the body, and cognition, including speech-accompanying gestures. Recently, she has also been exploring the fascinating world of R.

Poppy attended Elen Le Foll’s seminar “More than counting words: Introduction to statistics and data visualisation in R” (University of Cologne, summer 2024) as a guest student and wrote an earlier version of this chapter as part of this seminar. Elen contributed to the present revised version of this chapter.

Chapter overview

This chapter will guide you through the steps to reproduce the results of a published corpus linguistics study (Van Hulle & Enghels 2024a) using R.

The chapter will walk you through how to:

• Download the authors’ original data (Van Hulle & Enghels 2024b) and load it in R
• Understand the structure of the data
• Wrangle the data to reproduce Tables 5 and 8 from Van Hulle & Enghels (2024a)
• Calculate the normalized frequencies as reported in Van Hulle & Enghels (2024a)
• Calculate the type/token ratios as reported in Van Hulle & Enghels (2024a)
• Compare our results with those printed in Van Hulle & Enghels (2024a)
• Visualize our results as line plots using {ggplot2} to facilitate the interpretation of the results

14.1 Introducing the study

In this chapter, we attempt to reproduce the results of a corpus linguistics study by Van Hulle & Enghels (2024a), published as a book chapter in a volume edited by Pfadenhauer & Wiesinger (2024). The study focuses on the development of five throw verbs in Peninsular Spanish: echar, lanzar, disparar, tirar, and arrojar (Van Hulle & Enghels 2024a). These verbs have evolved into aspectual auxiliaries in inchoative constructions that convey the beginning of an event. Van Hulle & Enghels (2024a) use historical data to trace the evolution of these verbs, and contemporary data to analyse their usage in micro-constructions. Below are examples of the five throw verbs in inchoative constructions (all taken from Van Hulle & Enghels 2024a).

1. Los nuevos rebeldes se arrojaron a atacar al sistema de control social. (‘The new rebels started (lit. ‘threw/launched themselves’) to attack the system of social control.’)
2. El niño abrió los ojos y echó a correr de regreso a su casa. (‘The child opened his eyes and started (lit. ‘threw’) to run back to his house.’)
3. El grupo de investigación se lanzó a analizar otros parámetros. (‘The investigation group started (lit. ‘launched itself’) to analyse other parameters.’)
4. Decidí no tirarme a llorar y empecé a buscar algo que me ayudara. (‘I decided not to start (lit. ‘throw myself’) to cry and I started to look for something that would help me.’)
5. Y todos dispararon a correr, sin volver la cabeza atrás. (‘And everybody started (lit. ‘shot’) to run, without looking back.’)

Quiz time!

Follow the study’s DOI link and read the abstract to learn about the study’s research focus.

Van Hulle, Sven & Renata Enghels. 2024. The category of throw verbs as productive source of the Spanish inchoative construction. In Katrin Pfadenhauer & Evelyn Wiesinger (eds.), Romance motion verbs in language change, 213–240. De Gruyter. https://doi.org/10.1515/9783111248141-009.

Q1. What is the main focus of this study?

The relationship between inchoative constructions and nouns of motion.
The role of spatial expressions in the process of grammaticalization.
The development of 'throw' verbs as aspectual auxiliaries.
Semantic differences between the five Spanish 'throw' verbs.

Q2. According to the study, what semantic features help explain the connection between ‘throw’ verbs and inchoative constructions?

The ability of 'throw' verbs to convey accuracy and control.
The meaning of abruptness and the interruption of inertia.
The shift in meaning from the concrete to the abstract.
The aspect of moving towards a specified destination.

🐭 Click on the mouse for a hint.

In this chapter, we will use the authors’ original data to reproduce Tables 5 and 8 (Van Hulle & Enghels 2024a: 227, 232), as well as visualising the data with a series of informative line plots to facilitate interpretation.

14.2 Retrieving the authors’ original data

In the spirit of Open Science (see Section 1.1), Van Hulle & Enghels (2024a) have made their research data openly accessible on the Tromsø Repository of Language and Linguistics (TROLLing):

Van Hulle, Sven & Renata Enghels. 2024. Replication Data for: “The category of throw verbs as productive source of the Spanish inchoative construction.” DataverseNO. Version 1. https://doi.org/10.18710/TR2PWJ.

Follow the link and read the description of the dataset. Next, scroll down the page where three different downloadable files are listed.

• 0_ReadME_Spanish_ThrowVerbs_Inchoatives_20230413.txt This is a text “file which provides general information about the nature of the dataset and how the data was collected and annotated, and brief data-specific information for each file belonging to this dataset” (Van Hulle & Enghels 2024b).

• Spanish_ThrowVerbs_Inchoatives_20230413.csv This is a comma-separated file (see Section 2.5.1) which “contains the input data for the analysis, including the variables ‘AUX’, ‘Century’, ‘INF’ and ‘Class’, for the throw verbs arrojar, disparar, echar, lanzar and tirar” (Van Hulle & Enghels 2024b).

• Spanish_ThrowVerbs_Inchoatives_queries_20230413.txt “This file specifies all corpus queries”that were used to download the samples per auxiliary from the Spanish Web corpus (esTenTen18), that was accessed via Sketch Engine, and from the Corpus Diacrónico del Español (CORDE)” (Van Hulle & Enghels 2024b).

In corpus linguistics, it is often the case that corpora cannot be openly shared for copyright and/or data protection reasons. Instead, authors who strive to make their work transparent and reproducible can share details of the corpora that they analysed and of the specific corpus queries they used, so that the data that they share are only the results of the queries.

As we are interested in the frequencies retrieved from the corpora, we download the CSV file Spanish_ThrowVerbs_Inchoatives_20230413.csv.

Quiz time!

Q3. Where did the data for Van Hulle & Enghels (2024b)‘s study on the five Spanish ’throw’ verbs come from?

For the contemporary data, from the Spanish corpus of the Tromsø Repository of Language and Linguistics.
For all occurrences of 'throw' verbs, from the European Spanish Web Corpus (esTenTen18).
For the contemporary data, from the European Spanish subcorpus of the Spanish Web Corpus (esTenTen18).
For the historical data, from the Corpus Diacrónico del Español (CORDE).

🐭 Click on the mouse for a hint.

Q4. What does the term “false positive” refer to in the context of this study?

Tokens that represent infinitives following 'a' with an incorrect auxiliary.
Tokens removed due to being irrelevant to the study's focus on 'throw' verbs.
Tags that incorrectly label nouns as infinitives or misidentify inchoative constructions.
Tokens that were correctly identified as inchoative constructions.

14.3 ImpoRting the authors’ original data

Before we can import the dataset, we need to load all the packages that we will need for this project. Note that you may need to install some of these packages first (see Section 4.4.2 for instructions).

# Loading required packages for this project
library(here)
library(tidyverse)
library(xfun)

Next, we import the dataset containing the number of occurrences of ‘throw’ verbs in the corpora analysed in Van Hulle & Enghels (2024a) (Spanish_ThrowVerbs_Inchoatives_20230413.csv) as a new object called spanish.data. You will need to adjust the file path to match the folder structure of your computer (see Section 6.5).

# Importing the Spanish verbs dataset
spanish.data <- read.csv(file = here("data", "Spanish_ThrowVerbs_Inchoatives_20230413.csv"),
                    header = TRUE,
                    sep = "\t",
                    quote = "\"",
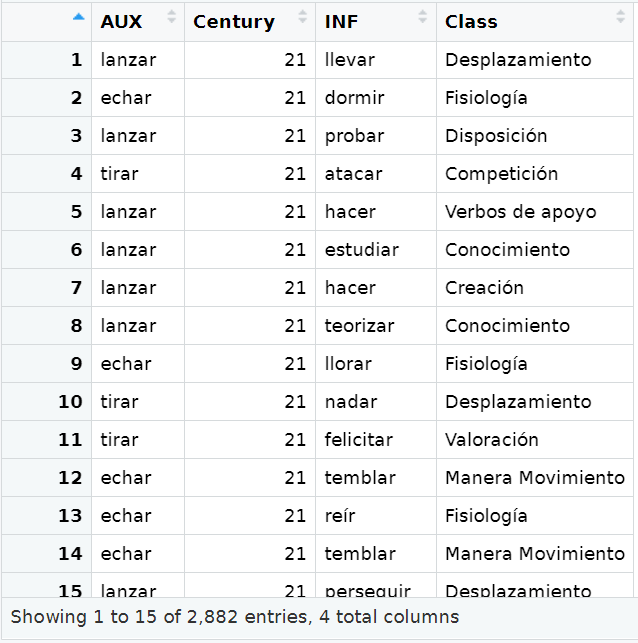
                    dec = ".")

We check the sanity of the imported data by visually examining the output of View(spanish.data) (Figure 14.1).

Figure 14.1: Screenshot showing part of the dataset using the View() function.

As you can see in Figure 14.1, the dataset contains 2882 rows (i.e., the number of occurrences of ‘throw’ verbs observed in the corpora) and 4 columns (i.e., variables describing these observations).

The readme file delivered with the data (0_ReadME_Spanish_ThrowVerbs_Inchoatives_20230413.txt) describes the variables as follows:

-----------------------------------------
DATA-SPECIFIC INFORMATION FOR: Spanish_ThrowVerbs_Inchoatives_20230413.csv
-----------------------------------------

#   Variable    Explanation

1   AUX         This column contains the inchoative auxiliary. [...]

2   Century     This column contains the century to which the concrete example belongs. 

3   INF         This column contains the infinitive observed in the filler slot of the inchoative construction. 

4   Class       This column contains the semantical class to which the infinitive belongs, based on the classification of ADESSE. This lexical classification classifies Spanish verbs in semantic groups, which we adopted for the annotation (http://adesse.uvigo.es/data) (@ref García-Miguel & Albertuz 2005). [...]

 

To obtain a list of all the ‘throw’ verbs included in the dataset and their total frequencies, we use the familiar count() function from {dyplr} (see Chapter 9).

spanish.data |> 
  count(AUX)

       AUX    n
1  arrojar  160
2 disparar    8
3    echar 1936
4   lanzar  680
5    tirar   98

As you can see, there are five ‘throw’ verbs in the dataset: echar, lanzar, tirar, arrojar, and disparar. The most frequent one is echar.

Quiz time!

Q5. Which column in the dataset contains the general meaning of the verbs in the filler slot of the inchoative construction?

AUX
INF
Century
Class

Q6. Which of the following verbs is classified under the semantic category ‘Desplazamiento’ (‘movement’)?

dormir
atacar
llevar
hacer

🐭 Click on the mouse for a hint.

14.4 Token (absolute) frequency

According to Gries & Ellis (2015: 232):

“Token frequency counts how often a particular form appears in the input.”

In Van Hulle & Enghels (2024a), token frequency refers to the number of occurrences of combinations of ‘throw’ verbs and infinitives in inchoative constructions, as identified in the corpora queried for this study (see Section 14.2).

14.4.1 Creating a table of token frequencies

First of all, we want to find out how often each ‘throw’ verb was observed in each century. To do so, we use the count() function to output the number of corpus occurrences for all possible combinations of the AUX and Century variables. Then, we pipe this output into an arrange() command to order the rows of the table by the values of the Century and AUX columns (as shown in Table 14.1 below), prioritising the order of the Century over the alphabetical order of the AUX. This ensures that the centuries are ordered correctly from the 13^th to the 21^st century, rather than being jumbled. We store this summary table (see Table 14.1) as a new R object called verbs.investigated.

verbs.investigated <- spanish.data |>
  count(AUX, Century, sort = TRUE) |> 
  arrange(Century, AUX)

Table 14.1 contains 26 rows and three columns, AUX, Century, both from the original dataset, and n which contains the number of occurrences for each combination of the Centuryand AUX variables. For example, the verb echar occurs 32, 15, and 101 times in the corpus data from the 13^th, 14^th, and 15^th centuries respectively and so on.

Table 14.1: Frequency of each Spanish ‘throw’ verb in each century

AUX	Century	n
echar	13	32
echar	14	15
echar	15	101
tirar	15	2
arrojar	16	20
echar	16	153
arrojar	17	47
disparar	17	3
echar	17	95
arrojar	18	16
echar	18	40
tirar	18	8
arrojar	19	38
disparar	19	1
echar	19	500
lanzar	19	55
arrojar	20	11
disparar	20	1
echar	20	500
lanzar	20	125
tirar	20	7
arrojar	21	28
disparar	21	3
echar	21	500
lanzar	21	500
tirar	21	81

We will now attempt to reproduce “Table 4: General overview of the dataset” (Van Hulle & Enghels 2024a: 225), reprinted below as Table 14.2.

Table 14.2: Absolute token frequency of Spanish ‘throw’ verbs as reported in van Hulle & Enghels (2024a: 225)

AUX	13	14	15	16	17	18	19	20	21	Total
arrojar	0	0	0	20	47	16	38	11	28	160
disparar	0	0	0	0	3	0	1	1	3	8
echar	32	15	101	153	95	40	500	500	500	1936
lanzar	0	0	0	0	0	0	55	125	500	680
tirar	0	0	0	0	0	0	0	7	81	88
Total	32	15	101	173	145	56	594	644	1112	2872

To reproduce this table on the basis of the data provided by the authors, we begin by reshaping the data frame spanish.data from long format to wide format using the pivot_wider() function (see Section 9.7). This function takes the arguments “names_from” to specify which column is to provide the names for the output columns, and “values_from” to determine which column is to supply the cell values.

verbs.investigated |>
  pivot_wider(names_from = Century, values_from = n) 

# A tibble: 5 × 10
  AUX       `13`  `14`  `15`  `16`  `17`  `18`  `19`  `20`  `21`
  <chr>    <int> <int> <int> <int> <int> <int> <int> <int> <int>
1 echar       32    15   101   153    95    40   500   500   500
2 tirar       NA    NA     2    NA    NA     8    NA     7    81
3 arrojar     NA    NA    NA    20    47    16    38    11    28
4 disparar    NA    NA    NA    NA     3    NA     1     1     3
5 lanzar      NA    NA    NA    NA    NA    NA    55   125   500

As you can see, this table includes a lot of NA values for the verbs for which zero occurrences were found in certain centuries. To replace missing values (NA) with a different value (here 0 to match Table 14.2), we can use the tidyverse function replace_na() in combination with mutate(). By applying this operation across(everything()), we ensure that the modifications are performed on all columns. We pipe this output into the arrange() function to order the rows of the table by the alphabetical order of the AUX. This is important as we will later use token.data to calculate the type/token frequency (see Table 14.11) for which we will merge token.data with the types.wide, which is also arranged by the alphabetical order of the AUX.

token.data <- verbs.investigated |>
  pivot_wider(names_from = Century, values_from = n) |> 
  mutate(across(everything(), ~ replace_na(., 0))) |>
  arrange(AUX) 

token.data

# A tibble: 5 × 10
  AUX       `13`  `14`  `15`  `16`  `17`  `18`  `19`  `20`  `21`
  <chr>    <int> <int> <int> <int> <int> <int> <int> <int> <int>
1 arrojar      0     0     0    20    47    16    38    11    28
2 disparar     0     0     0     0     3     0     1     1     3
3 echar       32    15   101   153    95    40   500   500   500
4 lanzar       0     0     0     0     0     0    55   125   500
5 tirar        0     0     2     0     0     8     0     7    81

We now want to add the total number of verb occurrences in each row and column of our table, as in (Van Hulle & Enghels 2024a, Table 4) (see also Table 14.2). We begin by calculating the total number of occurrences of each verb in token.data. We therefore first select just the columns containing numeric values.

numeric_columns <- token.data |> 
  select(where(is.numeric))

numeric_columns

# A tibble: 5 × 9
   `13`  `14`  `15`  `16`  `17`  `18`  `19`  `20`  `21`
  <int> <int> <int> <int> <int> <int> <int> <int> <int>
1     0     0     0    20    47    16    38    11    28
2     0     0     0     0     3     0     1     1     3
3    32    15   101   153    95    40   500   500   500
4     0     0     0     0     0     0    55   125   500
5     0     0     2     0     0     8     0     7    81

It is important that we specify that we only add the values in columns representing numeric variables because if we ask R to do any mathematical operations with values of the AUX variable, we will get an error message indicating that it is impossible to add up character string values!

sum(token.data$AUX)

Error in sum(token.data$AUX) : invalid 'type' (character) of argument

This is why we first created an R object that contains only the numeric variables of token.data: these are the columns that we will need to compute our sums. Next, we use the base R function rowSums() to calculate the total number of occurrences of each ‘throw’ verb across all corpus texts queried, from the 13^th to the 21^th century.

row_sums <- rowSums(numeric_columns)

We have saved the output of the rowSums() function to a new object called row_sums. This object is a numeric vector containing just the row totals.

row_sums

[1]  160    8 1936  680   98

To check that these are in fact the correct totals, we can compare these row sums to the output of table(spanish.data$AUX) (see also Section 14.3). As the numbers match, we can now use mutate() to add row_sums as a new column to token.data.

token.data.rowSums <- token.data |> 
  mutate(Total = row_sums)

token.data.rowSums

# A tibble: 5 × 11
  AUX       `13`  `14`  `15`  `16`  `17`  `18`  `19`  `20`  `21` Total
  <chr>    <int> <int> <int> <int> <int> <int> <int> <int> <int> <dbl>
1 arrojar      0     0     0    20    47    16    38    11    28   160
2 disparar     0     0     0     0     3     0     1     1     3     8
3 echar       32    15   101   153    95    40   500   500   500  1936
4 lanzar       0     0     0     0     0     0    55   125   500   680
5 tirar        0     0     2     0     0     8     0     7    81    98

Now, let’s turn to the column totals. We can use colSums() to calculate the total number of ‘throw’ verb occurrences in each century.

column_sums <- colSums(numeric_columns)

column_sums

  13   14   15   16   17   18   19   20   21 
  32   15  103  173  145   64  594  644 1112 

In the original paper, the row of totals is labelled “Total”. Furthermore, we also have a value representing the total number of verbs included in the dataset. Hence, the last row will be constructed as follows using the combine function c().

total_row <- c("Total", column_sums, sum(row_sums))

total_row

             13      14      15      16      17      18      19      20      21 
"Total"    "32"    "15"   "103"   "173"   "145"    "64"   "594"   "644"  "1112" 
        
 "2882" 

Again, we can check that we have not “lost” any verbs along the way by comparing the last value of total_row with the number of observations in our original long-format dataset.

nrow(spanish.data)

[1] 2882

Finally, we use rbind() to append the total_row vector to token.data, creating a complete table with both row and column totals (Table 14.3).

Table 14.3: Absolute token frequency of Spanish ‘throw’ verbs based on dataset

token.table.totals <- rbind(token.data.rowSums, total_row)

token.table.totals

# A tibble: 6 × 11
  AUX      `13`  `14`  `15`  `16`  `17`  `18`  `19`  `20`  `21`  Total
  <chr>    <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr>
1 arrojar  0     0     0     20    47    16    38    11    28    160  
2 disparar 0     0     0     0     3     0     1     1     3     8    
3 echar    32    15    101   153   95    40    500   500   500   1936 
4 lanzar   0     0     0     0     0     0     55    125   500   680  
5 tirar    0     0     2     0     0     8     0     7     81    98   
6 Total    32    15    103   173   145   64    594   644   1112  2882 

If we now compare the values of the table in the published study (reproduced as Table 14.2) with Table 14.3 based on the authors’ archived data, we can see that the total number of ‘throw’ verbs is only 2872, suggesting that ten verb occurrences are somehow missing in the summary table printed in the published paper. In the data frame spanish.data, these missing data points correspond to occurrences of the verb tirar, specifically two tokens from the 15^th century and eight tokens from the 18^th century (Table 14.3).

Since Van Hulle & Enghels (2024a) focus their analyses on the other two verbs, echar and lanzar, this discrepancy is not particularly conspicuous. However, it suggests that the version of the dataset archived on TROLLing is not exactly the same as the one that the authors presumably used for the analyses presented in the 2024 paper.¹

14.4.2 Visualising the absolute frequencies in a tabular format

As Van Hulle & Enghels (Van Hulle & Enghels 2024a: 224) state,

“The searches in the databases of CORDE and esTenTen18 were exhaustive, but, for reasons of feasibility, only the first 500 relevant cases were included in the final dataset.”

That is, the corpus contains much more data than what the authors could feasibly investigate. For example, the verb echar appears 799 times in the 19^th century texts, 1,641 times in the 20^th texts, and 10,347 times in those from the 21^st century. However, in their final dataset Van Hulle & Enghels (2024a) included only 500 instances of echar in these centuries, as shown in Table 14.2 above.

To generate a table that includes the absolute token frequency in the corpus, similar to the “absolute token frequency” subsection of Table 5 in Van Hulle & Enghels (Van Hulle & Enghels 2024a: 227), we need to modify the values of echar in the 19^th, 20^th, and 21^st centuries, and lanzar in the 21^st century in verbs.investigated that we previously created.

We use the mutate() function to update specific columns and case_when() to define the conditions of the changes. For example, if the verb echar appears in the AUX variable and at the same time the value 19 is found in the Century variable, then the cell value should be changed to 799, and so on. The formula TRUE ~ n ensures that the original value is retained if no condition is met. The modified table is assigned to a new data frame object, which we name verbs.corpus.

Next, we generate a contingency table with the altered values for those verbs by applying the pivot_wider() function as in Table 14.3 above. The result is displayed in Table 14.4 below.

verbs.corpus <- verbs.investigated |>
  # Modifying specific columns with mutate()
  mutate(n = case_when(
    AUX == "echar" & Century == 19 ~ 799,
    AUX == "echar" & Century == 20 ~ 1641,
    AUX == "echar" & Century == 21 ~ 10347,
    AUX == "lanzar" & Century == 21 ~ 7625,
    # Keep the original value if no condition is met
    TRUE ~ n))

# Generating a contingency table with the altered verb values using pivot_wider()
verbs.corpus.wide <- verbs.corpus |>
  pivot_wider(names_from = Century, values_from = n) |>
  mutate(across(everything(), ~ replace_na(., 0))) |>
  arrange(AUX)

verbs.corpus.wide

Table 14.4: Absolute token frequency of Spanish ‘throw’ verbs as observed in the corpus

# A tibble: 5 × 10
  AUX       `13`  `14`  `15`  `16`  `17`  `18`  `19`  `20`  `21`
  <chr>    <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 arrojar      0     0     0    20    47    16    38    11    28
2 disparar     0     0     0     0     3     0     1     1     3
3 echar       32    15   101   153    95    40   799  1641 10347
4 lanzar       0     0     0     0     0     0    55   125  7625
5 tirar        0     0     2     0     0     8     0     7    81

The difference between the corpus data (Table 14.4) and the final dataset (Table 14.3) is found only in echar in 19^th, 20^th, 21^st, and in lanzar in 21^st centuries. Following Van Hulle & Enghels (2024a), we will use the frequency of Spanish ‘throw’ verbs (stored as a data frame named verbs.corpus) observed in the corpus (Table 14.4) to calculate the normalized frequency (see Table 14.7 below).

14.5 Normalized frequency

A normalized frequency is an occurrence rate adjusted to a common base, such as per million words (pmw), to allow comparisons across datasets of different sizes.

Van Hulle & Enghels (2024a) analyse Spanish corpora from different centuries, using the Corpus Diacrónico del Español (CORDE) for the 13^th to 20^th centuries and the esTenTen18 corpus for the 21^st century, accessed via the Sketch Engine platform. To compare frequencies from these varying-sized corpora, we need to normalize them to ensure that large frequencies are not simply due to the corpus being larger. Van Hulle & Enghels (Van Hulle & Enghels 2024a: 227, footnote 2) explain:

The normalised token frequencies are calculated dividing the absolute token frequency by these total amounts of words, multiplied by 1 million. This number then shows how many times each micro-construction occurs per 1 million words, per century.

The formula for normalized frequency is as follows:

\[ normalized frequency = \frac{token frequency}{total words *1000000} \]

14.5.1 Visualising normalized frequencies in a tabular format

We will now attempt to reproduce the “Normalized Token Frequency” sections of Tables 5 and 8 from the published paper using the authors’ original data. For later comparison, the normalized frequencies as reported in Van Hulle & Enghels (Van Hulle & Enghels 2024a: 227, 232)² are reproduced in this chapter as Table 14.5.

Table 14.5: Normalized frequency (pmw) as reported in the published paper (Van Hulle & Enghels 2024a: Tables 5 and 8)

AUX	13	14	15	16	17	18	19	20	21
arrojar	-	-	-	0.4	1.23	1.11	0.89	0.19	0.01
disparar	-	-	-	-	0.08	-	0.02	0.02	0.0008
echar	4.09	2	4.43	3.07	2.49	2.76	18.7	27.96	2.91
lanzar	-	-	-	-	-	-	1.31	2.15	2.14
tirar	-	-	-	-	-	-	-	0.12	0.02

The sizes of the corpora for each century are provided in Van Hulle & Enghels (Van Hulle & Enghels 2024a: 227, footnote 12)³. We create a table of word counts for each century (Table 14.6) using the tibble() function from the tidyverse, by concatenating (using the c() function) the values of Words and Century and storing these as a new data frame named corpus_sizes.

corpus_sizes <- tibble(Century = c(13, 14, 15, 16, 17, 18, 19, 20, 21),
                       Words = c(7829566, 7483952, 22796824, 49912675, 38083322, 14466748, 42726881, 58686214, 3554986755))

Table 14.6: Total numbers of words in the corpora

corpus_sizes

# A tibble: 9 × 2
  Century      Words
    <dbl>      <dbl>
1      13    7829566
2      14    7483952
3      15   22796824
4      16   49912675
5      17   38083322
6      18   14466748
7      19   42726881
8      20   58686214
9      21 3554986755

We will apply this formula to each verb for every century. First, we use the left_join function from {dplyr} to combine two data frames, i.e. verbs.corpus, which we used to create Table 14.4, and corpus_sizes, which we just created (Table 14.6), based on the common Century column.

left_join(verbs.corpus, corpus_sizes, by = "Century")

        AUX Century     n      Words
1     echar      13    32    7829566
2     echar      14    15    7483952
3     echar      15   101   22796824
4     tirar      15     2   22796824
5   arrojar      16    20   49912675
6     echar      16   153   49912675
7   arrojar      17    47   38083322
8  disparar      17     3   38083322
9     echar      17    95   38083322
10  arrojar      18    16   14466748
11    echar      18    40   14466748
12    tirar      18     8   14466748
13  arrojar      19    38   42726881
14 disparar      19     1   42726881
15    echar      19   799   42726881
16   lanzar      19    55   42726881
17  arrojar      20    11   58686214
18 disparar      20     1   58686214
19    echar      20  1641   58686214
20   lanzar      20   125   58686214
21    tirar      20     7   58686214
22  arrojar      21    28 3554986755
23 disparar      21     3 3554986755
24    echar      21 10347 3554986755
25   lanzar      21  7625 3554986755
26    tirar      21    81 3554986755

Next, we pipe the combined data frames into a mutate() function to add a new column named normalized and apply the formula (n / Words) * 1000000 to normalize the frequency. In a second step, we round the result to two decimal places.

left_join(verbs.corpus, corpus_sizes, by = "Century") |>
  mutate(normalized = (n / Words) * 1000000) |>
  mutate(normalized = round(normalized,
                            digits = 2))

        AUX Century     n      Words normalized
1     echar      13    32    7829566       4.09
2     echar      14    15    7483952       2.00
3     echar      15   101   22796824       4.43
4     tirar      15     2   22796824       0.09
5   arrojar      16    20   49912675       0.40
6     echar      16   153   49912675       3.07
7   arrojar      17    47   38083322       1.23
8  disparar      17     3   38083322       0.08
9     echar      17    95   38083322       2.49
10  arrojar      18    16   14466748       1.11
11    echar      18    40   14466748       2.76
12    tirar      18     8   14466748       0.55
13  arrojar      19    38   42726881       0.89
14 disparar      19     1   42726881       0.02
15    echar      19   799   42726881      18.70
16   lanzar      19    55   42726881       1.29
17  arrojar      20    11   58686214       0.19
18 disparar      20     1   58686214       0.02
19    echar      20  1641   58686214      27.96
20   lanzar      20   125   58686214       2.13
21    tirar      20     7   58686214       0.12
22  arrojar      21    28 3554986755       0.01
23 disparar      21     3 3554986755       0.00
24    echar      21 10347 3554986755       2.91
25   lanzar      21  7625 3554986755       2.14
26    tirar      21    81 3554986755       0.02

Next, we remove the n and Words columns that we no longer need here by combining the minus operator - and the select() function to “unselect” these columns.

verb.normalized <- left_join(verbs.corpus,
                           corpus_sizes,
                           by = "Century") |>
  mutate(normalized = (n / Words) * 1000000) |>
  mutate(normalized = round(normalized,
                          digits = 2)) |> 
  select(-c(n, Words))

verb.normalized

        AUX Century normalized
1     echar      13       4.09
2     echar      14       2.00
3     echar      15       4.43
4     tirar      15       0.09
5   arrojar      16       0.40
6     echar      16       3.07
7   arrojar      17       1.23
8  disparar      17       0.08
9     echar      17       2.49
10  arrojar      18       1.11
11    echar      18       2.76
12    tirar      18       0.55
13  arrojar      19       0.89
14 disparar      19       0.02
15    echar      19      18.70
16   lanzar      19       1.29
17  arrojar      20       0.19
18 disparar      20       0.02
19    echar      20      27.96
20   lanzar      20       2.13
21    tirar      20       0.12
22  arrojar      21       0.01
23 disparar      21       0.00
24    echar      21       2.91
25   lanzar      21       2.14
26    tirar      21       0.02

We reshape the data frame verb.normalized from long format to wide format by replicating the pivot_wider() function, which we used to create Table 14.2 and Table 14.4. The new column names will be taken from Century. The values in the new column will come from normalized. As earlier, we sort the rows of the data frame according to the alphabetical order of AUX using arrange(). We convert the output into a data frame format with the as.data.frame() command and assign the output to normalized.wide.

normalized.wide <- verb.normalized |>
  pivot_wider(names_from = Century, values_from = normalized) |>
  arrange(AUX) |> 
  as.data.frame()

normalized.wide

       AUX   13 14   15   16   17   18    19    20   21
1  arrojar   NA NA   NA 0.40 1.23 1.11  0.89  0.19 0.01
2 disparar   NA NA   NA   NA 0.08   NA  0.02  0.02 0.00
3    echar 4.09  2 4.43 3.07 2.49 2.76 18.70 27.96 2.91
4   lanzar   NA NA   NA   NA   NA   NA  1.29  2.13 2.14
5    tirar   NA NA 0.09   NA   NA 0.55    NA  0.12 0.02

Next, we use the is.na() function to find all missing values (NA) in the data frame normalized.wide. We replace all these NA values with a dash ("-") using the <- operator.

normalized.wide[is.na(normalized.wide)] <- "-"

The result can be seen in Table 14.7.

# Use left_join to merge the dataframes
verb.normalized <- left_join(verbs.corpus,
                             corpus_sizes,
                             by = "Century") |>
# Use mutate to create a new column with n divided by words
  mutate(normalized = (n / Words) * 1000000) |>
  mutate(normalized = round(normalized,
                            digits = 2)) |> 
# Remove raw frequencies (n) and corpus sizes (Words)
  select(-c(n, Words))

# Pivot to wide format and replace NAs with 0
normalized.wide <- verb.normalized |>
  pivot_wider(names_from = Century, values_from = normalized) |>
  arrange(AUX) |> 
  as.data.frame()

# replace NA with "-"
normalized.wide[is.na(normalized.wide)] <- "-"

normalized.wide

Table 14.7: Normalized frequency of Spanish ‘throw’ verbs (pmw) based on TROLLing data

       AUX   13 14   15   16   17   18   19    20   21
1  arrojar    -  -    -  0.4 1.23 1.11 0.89  0.19 0.01
2 disparar    -  -    -    - 0.08    - 0.02  0.02 0.00
3    echar 4.09  2 4.43 3.07 2.49 2.76 18.7 27.96 2.91
4   lanzar    -  -    -    -    -    - 1.29  2.13 2.14
5    tirar    -  - 0.09    -    - 0.55    -  0.12 0.02

At this stage, it is important to note some differences between Table 14.7 and Table 14.5. Van Hulle & Enghels (2024a) provided normalized frequencies for the three verbs arrojar, disparar and tirar only from the 16^th until the 21^st centuries, with no data for the 13^th to 15^th centuries. However, Table 14.7 shows the normalized frequency of tirar at 0.09 for the 15^th century and 0.55 for the 18^th century, filling in some missing data found in the dataset (Table 14.3). Additionally, there are slight differences in the normalized frequencies of lanzar for the 19^th and 20^th centuries, calculated as 1.29 and 2.13 based on TROLLing data and displayed in Table 14.7, compared to 1.31 and 2.15 in reported by Van Hulle & Enghels (2024a) and displayed in Table 14.5.

Another point to note is the apparent discrepancy in the normalized frequency of the verb disparar. In Table 14.5, it is reported in the original paper as 0.0008 for the 21^st century, while Table 14.7 displays it as 0.00. However, this difference is due to Table 14.7 using a two-digit format; when rounded to four digits, the value would indeed be 0.0008. Thus, this is not a true discrepancy.

14.5.2 Visualisation of the normalized frequencies as a line graph

We now visualize how the usage of Spanish ‘throw’ verbs in inchoative constructions has evolved from the 13^th to the 21^st century. Although such a visualization is not provided in Van Hulle & Enghels (2024a), it is mentioned in the dataset description Van Hulle & Enghels (2024b), and it can facilitate the interpretation of the changes in normalized frequencies documented in Table 14.7.

For a diachronic study based on corpus data, it is reasonable to choose a connected scatterplot, which is essentially a combination of a scatterplot and a line plot. Using the {ggplot2} package, this entails combining a geom_point() layer on top of a geom_line() layer. The connected scatterplot provides a visualisation that helps to identify the usage of the five ‘throw’ verbs in inchoative constructions over time.

Figure 14.2 is created using a ggplot() function that takes the data frame verb.normalized as its first argument and the aesthetics (aes) as its second argument. For the aes argument, we choose the Century column for the x-axis and the column normalized for the y-axis. Additionally, we specify two more optional aesthetics mappings in aes: “color” and “group”. Both will be mapped onto the AUX variable, meaning that each verb will be displayed in a different color, and the line will be grouped by each verb over time. We also add a scale_x_continuous() layer ensures that the x-axis is labelled from the 13^th to 21^st century.

ggplot(verb.normalized, 
       aes(x = Century, 
           y = normalized, 
           color = AUX, 
           group = AUX)) +
  geom_point() +  # Scatterplot points
  geom_line() +   # Connect points with lines
  scale_x_continuous(breaks = 13:21) + 
  labs(title = "Normalized frequency of Spanish 'throw' verbs over time",
       x = "Century",
       y = "Normalized frequency (pmw)",
       color = "Verbs") +
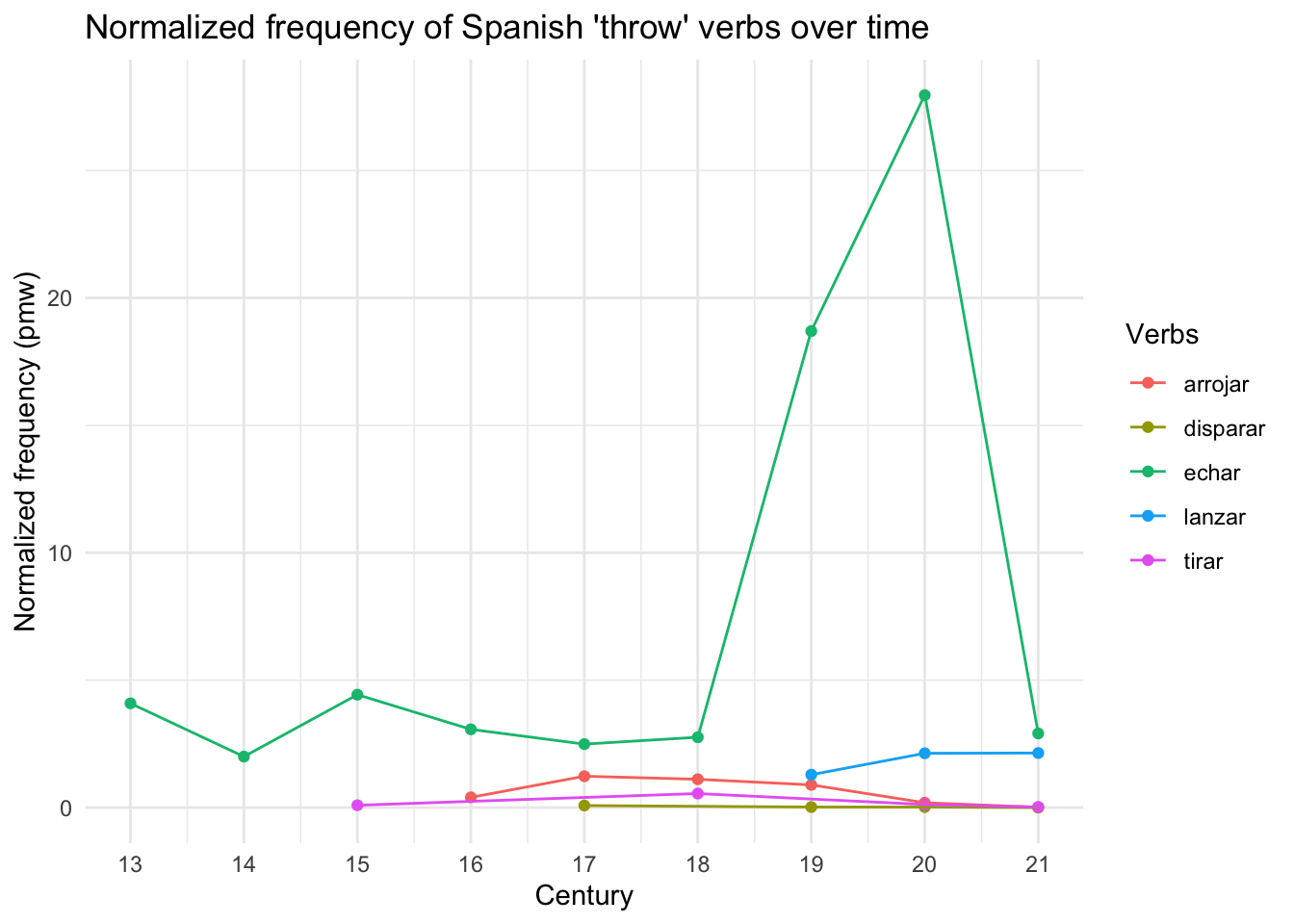
  theme_minimal()

Figure 14.2: Normalized frequency of Spanish ‘throw’ verbs over time

Figure 14.2 shows that the verb echar is the most frequently used verb as an inchoative auxiliary, appearing in the corpus since the 13^th century, while the other verbs only began to appear from the 15^th century (tirar), the 16^th century (arrojar), the 17^th century (disparar), and the 19^th century (lanzar). According to Van Hulle & Enghels (2024a: 223), the verb echar “can be considered as the exemplary verb which opened the pathway for other ‘throw’ verbs towards the aspectual inchoative domain”. They further state, > “The relative token frequency increases remarkably in the 19th (n=18,70) and 20th (n=27,96) centuries, which can thus be defined as the time frames in which the micro-construction with echar was most frequently used. In the 21st century data, both micro-constructions appear with a comparable normalized token frequency in the corpus” (Van Hulle & Enghels (2024a)).

The normalized frequency graphic of Spanish ‘throw’ verbs in Figure 14.2 effectively illustrates the authors’ statement, providing a clear visual representation of how these verbs have evolved in usage over time.

14.6 Type frequency

Type frequency refers to the number of unique words that can appear in a specific position, or “slot,” within a particular grammatical construction. In the context of an inchoative construction, a specific slot refers to the position within the construction where an infinitive verb can occur.

For example, let’s look at the data in spanish.data (as shown in View(spanish.data) in the imported data, (see Figure 14.1). Here, we see a list of verb usages, with each row representing a token, or instance, of a verb in a sentence or construction. There are 15 rows, each representing a token of a verb in specific sentences.

If we focus on the verb lanzar, we can count a total of 7 tokens, meaning that lanzar appears 7 times in Figure 14.1 (in the 1^st, 3^rd, 5^th, 6^th, 7^th, 8^th, and 15^th rows). However, among these tokens, lanzar pairs twice with hacer in an inchoative construction. Because hacer is repeated, this combination with lanzar is counted as only one type. Therefore, although we have 7 tokens (occurrences) of lanzar, we have only 6 unique types (distinct pairings) involving lanzar in the inchoative slot.

Van Hulle & Enghels (2024a: 226) state that one may generally assume “that a higher type frequency indicates a higher degree of semantic productivity. As such, it is likely that a construction with a high number of different infinitives will accept even more types in the future”. Thus, type frequency is an important measure of how productive and adaptable a pattern is.

14.6.1 Visualising type frequencies in a tabular format

We will now attempt to reproduce the type frequencies of Spanish ‘throw’ verbs as displayed in the two subtables (both labelled “type frequency”) of the original publication: one for echar and lanzar (Van Hulle & Enghels 2024a: Table 5) and the other for arrojar, disparar and tirar (Van Hulle & Enghels 2024a: Table 8). The values from these two subtables are reproduced in this chapter as Table 14.8.

Table 14.8: Type frequency of Spanish ‘throw’ verbs based on the published paper

AUX	13	14	15	16	17	18	19	20	21
arrojar	-	-	-	16	34	13	32	10	27
disparar	-	-	-	-	2	-	1	1	3
echar	8	3	15	12	12	17	19	20	20
lanzar	-	-	-	-	-	-	45	95	215
tirar	-	-	-	-	-	-	-	7	46

Based on the object spanish.data (see Figure 14.1), which we created from on the TROLLing dataset Spanish_ThrowVerbs_Inchoatives_20230413.csv, we can calculate the type frequency of each ‘throw’ verbs in inchoative construction (see Table 14.9). To achieve this, we first select the first three columns of spanish.data, i.e. AUX, Century, INF. The result is a long table with the three columns and 2,882 rows. We check the first six lines of the table using the head() function.

type.token <- select(spanish.data, 1:3)
head(type.token)

     AUX Century      INF
1 lanzar      21   llevar
2  echar      21   dormir
3 lanzar      21   probar
4  tirar      21   atacar
5 lanzar      21    hacer
6 lanzar      21 estudiar

We then calculate the number of unique combinations among these variables using the distinct() function. We pipe the output into a group_by() function, which allows us to group all the corpus occurences according to Century and AUX. Then, using the summarize() function, we create a new column called Types with the number (n) of types corresponding to each combination of Century and AUX. We convert the output into a data frame format using as.data.frame() and assign it to a new R object called verb.types.

verb.types <- type.token |> 
  distinct(Century, AUX, INF) |> 
  group_by(Century, AUX) |> 
  summarize(Types = n()) |> 
  as.data.frame()

We reshape the object verb.types from long format to wide format using the pivot_wider() function. The new column names will be taken from Century. The values in the new column will come from Types. We use mutate(across(everything()) to modify all columns at once. The modification entails replacing all missing values (NA) with 0 using the replace_na function. Next, we sort the rows of the data frame in the alphabetical order of the AUX column using the arrange() function. We assign the output to types.wide.

types.wide <- verb.types |>
  pivot_wider(names_from = Century, values_from = Types) |>
  mutate(across(everything(), ~ replace_na(., 0))) |>
  arrange(AUX)

The result is displayed as Table 14.9.

# Selecting the first three columns of spanish.data
# Creating a type frequency table labelled as type.token
type.token <- select(spanish.data, 1:3)

# Calculating distinct combinations of Century, AUX, and INF using the distinct() function
# Grouping data by Century and AUX using the group_by() function
# Creating a new column Types with the summarize() function,
# Returning the count (n) for each group

verb.types <- type.token |> 
  distinct(Century, AUX, INF) |> 
  group_by(Century, AUX) |> 
  summarize(Types = n())

# Converting verb.types to a data frame using the as.data.frame() function
verb.types <- as.data.frame(verb.types)

# Using the pivot_wider() function to create a contigency table
types.wide <- verb.types |>
  pivot_wider(names_from = Century, values_from = Types) |>
  mutate(across(everything(), ~ replace_na(., 0))) |>
  arrange(AUX)

# Printing the table in elegantly formatted HTML format
types.wide

Table 14.9: Type frequency of Spanish ‘throw’ verbs based on data

# A tibble: 5 × 10
  AUX       `13`  `14`  `15`  `16`  `17`  `18`  `19`  `20`  `21`
  <chr>    <int> <int> <int> <int> <int> <int> <int> <int> <int>
1 arrojar      0     0     0    16    34    13    32    10    27
2 disparar     0     0     0     0     2     0     1     1     3
3 echar        8     3    15    12    12    17    18    22    20
4 lanzar       0     0     0     0     0     0    44    95   215
5 tirar        0     0     2     0     0     7     0     7    46

Here, too, we observe several discrepancies between Table 14.9 and Table 14.8. The discrepancies involve the type frequencies of echar for the 19^th and 20^th centuries, reported as 19 and 20 in the original paper, and of lanzar for the 19^th century, originally reported as 45 (Table 14.8). Other discrepancies include the type frequencies of the verb tirar in the 15^th and 18^th centuries, which are two and seven according to the TROLLing data, but both reported as zero in the published study (see also Table 14.2).

14.6.2 Visualisation of the type frequency as a line graph

Using the type frequency data that we calculated above (see Table 14.9), we can largely recycle the ggplot() code that we used to create Figure 14.2.

# Using the ggplot() function with the dataframe verb.types
# The y-axis represents the type frequency
ggplot(verb.types, 
       aes(x = Century, 
           y = Types, 
           color = AUX, 
           group = AUX)) +
  geom_point() +  # Scatterplot points
  geom_line() +   # Connect points with lines
  scale_x_continuous(breaks = 13:21) + 
  labs(title = "Productivity of Spanish 'throw' verbs over time",
       x = "Century",
       y = "Type frequency",
       color = "Verbs") +
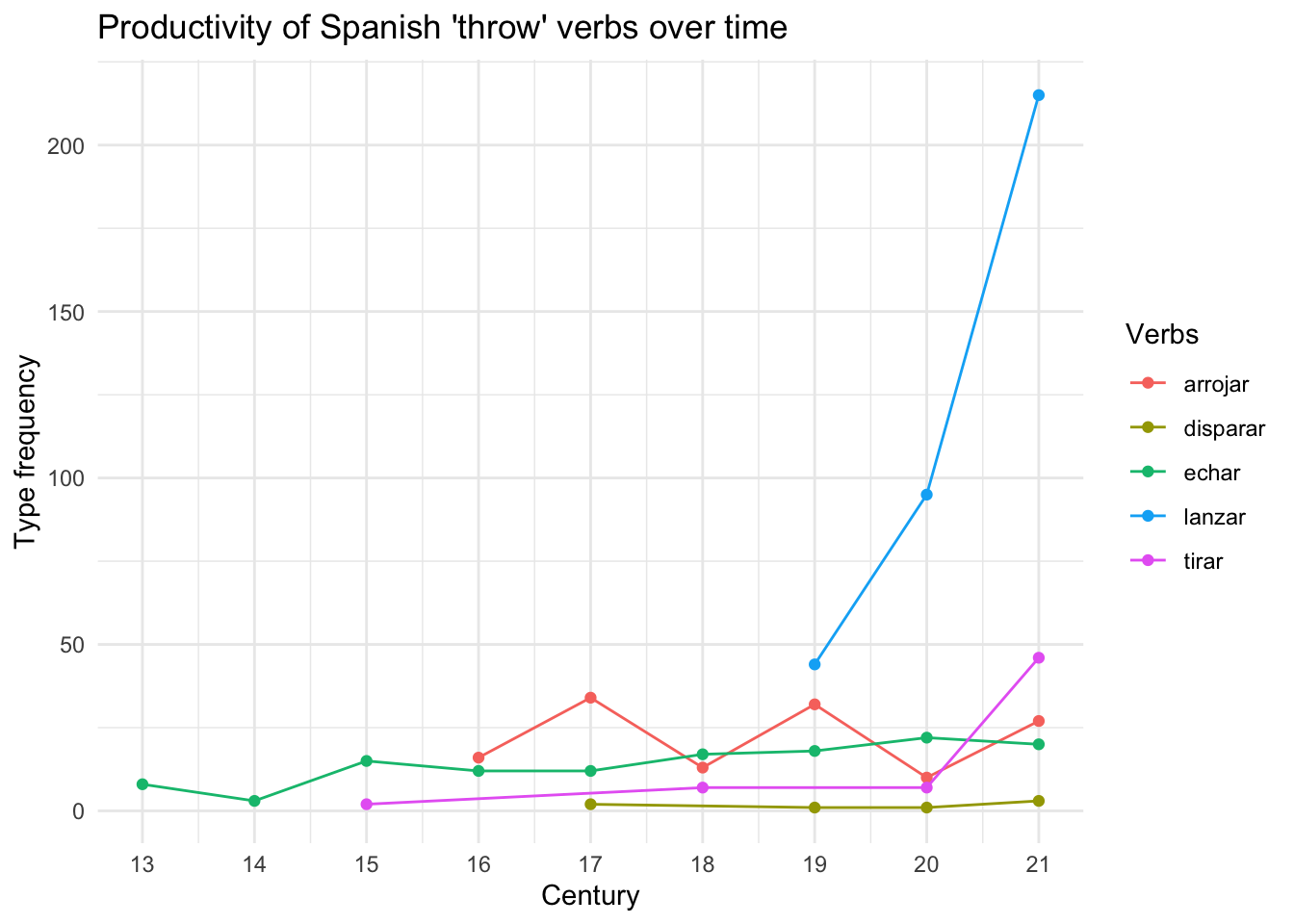
  theme_minimal()

Figure 14.3: Type frequency of Spanish ‘throw’ verbs over time

The connected scatterplot displayed in Figure 14.3 provides a visualisation that helps identify the productivity of the five ‘throw’ verbs in inchoative constructions with respect to their type frequency.

As Van Hulle & Enghels (2024a: 226) state:

“In general, it is assumed that a higher type frequency indicates a higher degree of semantic productivity. As such, it is likely that a construction with a high number of different infinitives will accept even more types in the future. In this sense, type frequency constitutes an important parameter to measure the extending productivity of a construction”.

However, we should interpret this graphic carefully, keeping in mind that absence of evidence is not evidence of absence. Notably, there is almost no data for disparar, which raises the question: in the real world, is this verb rarely used in an inchoative construction, or are there simply no examples in the corpus?

Quiz time!

Q7. Which line of code can you add in the ggplot() code above to change the color scheme of the line graph in Figure 14.3 to a color-blind friendly one? Click on “Show the R code to generate the graph below.” to see the code for Figure 14.3.

+ scale_color_viridis_b()
+ scale_color_continuous()
+ scale_color_viridis_d()
+ scale_color_viridis_c()
+ scale_color_blind()

🐭 Click on the mouse for a hint.

Q8. Alternatively, we could opt for a black-and-white solution like below. How can we adapt the ggplot() code from Figure 14.3 to achieve this?

Change `aes(color = AUX)` to `aes(linetype = AUX)`
Change `aes(color = AUX)` to `aes(line = AUX)`
Change `geom_line()` to `geom_line(linetype = AUX)`
Change `geom_line()` to `geom_dotted()`

14.7 Type/token ratio (TTR)

As stated by Van Hulle & Enghels (2024a: 226), the “type/token ratio measures the realized productivity” of each verb. Furthermore,

since type frequency depends to some extent on token frequency (the more tokens, the more opportunities for different types to occur), the two must be put into some kind of relationship. The simplest measure suggested in the literature is the type/token ratio […] (Stefanowitsch & Flach 2017: 118)

Type/token ratios (TTR) can range from zero and one. A TTR of zero indicates that there are no examples of the type in the given occurrences, while a TTR of one signifies that all types are unique to those given occurrences.

\[ TTR = \frac{types}{tokens} \]

As type/token ratios depend on corpus size, Van Hulle & Enghels (2024a: 227) explain that:

“To be representative, the measures of type/token and hapax/token ratio are calculated on a maximum of 500 tokens per auxiliary. Specifically, for echar in the 19^th, 20^th and 21^st century and for lanzar in the 21^st century, token frequency is reduced to 500.”

14.7.1 Visualising type/token ratios in a tabular format

We will now attempt to reproduce the type/token ratio of Spanish throw verbs based on two subtables (both labelled “type/token ratio”): one for echar and lanzar (Table 5 from Van Hulle & Enghels 2024a: 227) and the other for arrojar, disparar and tirar (Table 8 from Van Hulle & Enghels 2024a: 232), which are reproduced in this chapter as Table 14.10.

Table 14.10: Type/token ratio of Spanish ‘throw’ verbs over time based on Van Hulle & Enghels (2024a)

AUX	13	14	15	16	17	18	19	20	21
arrojar	-	-	-	0.8	0.72	0.81	0.84	0.91	0.96
disparar	-	-	-	-	0.67	-	1	1.00	1.00
echar	0.25	0.2	0.15	0.08	0.13	0.43	0.04	0.04	0.04
lanzar	-	-	-	-	-	-	0.8	0.75	0.43
tirar	-	-	-	-	-	-	-	1.00	0.57

To calculate type/token ratios, we first create two matching wide tables, one for the token frequencies, and another for the type frequencies. We can use the wide table labelled token.data from Table 14.3, and the wide table labelled types.wide from Table 14.9 as they are ordered in exactly the same way (you can check this by comparing their structures using the str() function).

First, we create a new data frame using the data.frame() function. This data frame will take its first column from token.data, which contains the auxiliary verbs (AUX). We access this column using token.data[, 1].⁴

Next, we calculate the type/token ratio. This is done by dividing the numeric values in types.wide (i.e., all columns except the first) by the corresponding values in token.data. To this end, we use the notation types.wide[, -1] / token.data[, -1]. The [, -1] indicates that we take all columns except the first one. We exclude the first column because it contains non-numeric values (the AUX column).

Finally, we combine these components into our new data frame. We include the AUX column as the first column by selecting it with the command token.data[, 1]. To ensure that the column names remain unchanged, we set check.names = FALSE in the data.frame() function. This prevents R from altering the original column names, keeping them exactly as they are in token.data. We also round() the values of all numeric columns to just two decimals.

data.frame(token.data[, 1], 
           types.wide[, -1] / token.data[, -1],
           check.names = FALSE) |> 
    mutate(across(where(is.numeric), round, digits = 2))

       AUX   13  14   15   16   17   18   19   20   21
1  arrojar  NaN NaN  NaN 0.80 0.72 0.81 0.84 0.91 0.96
2 disparar  NaN NaN  NaN  NaN 0.67  NaN 1.00 1.00 1.00
3    echar 0.25 0.2 0.15 0.08 0.13 0.42 0.04 0.04 0.04
4   lanzar  NaN NaN  NaN  NaN  NaN  NaN 0.80 0.76 0.43
5    tirar  NaN NaN 1.00  NaN  NaN 0.88  NaN 1.00 0.57

Our table contains a lot NaN values. In these cells of the table, the number of tokens was zero and, as a consequence, the number of types was also zero. As it is mathematically impossible to divide zero by zero, R returns NaN values instead. To replace these NaN values to dashes ("-") to match the formatting of the published tables, we use the base R function is.na().

type.token1 <- data.frame(token.data[, 1], 

                          types.wide[, -1] / token.data[, -1],

                          check.names = FALSE) |> 
    mutate(across(where(is.numeric), round, digits = 2))

type.token1[is.na(type.token1)] <- "-"

The result is saved as type.token1 and is displayed below as Table 14.11.

Table 14.11: Type/token ratio of Spanish ‘throw’ verbs over time based on data

       AUX   13  14   15   16   17   18   19   20   21
1  arrojar    -   -    -  0.8 0.72 0.81 0.84 0.91 0.96
2 disparar    -   -    -    - 0.67    -    1 1.00 1.00
3    echar 0.25 0.2 0.15 0.08 0.13 0.42 0.04 0.04 0.04
4   lanzar    -   -    -    -    -    -  0.8 0.76 0.43
5    tirar    -   -    1    -    - 0.88    - 1.00 0.57

Comparing Table 14.10 and Table 14.11, we find some minor discrepancies between the type/token ratios presented in the published paper and those calculated on the basis of the TROLLing data. The type/token ratio of the verb tirar in the 15^th and 18^th centuries, are reported as 0 and 0 in the published paper (see also Table 14.10), but as 1 and 0.88 in Table 14.11. These differences correspond to the discrepancies already identified when calculating the token frequencies (see Section 14.4.1).

The other (very minor) discrepancies involve the type/token ratio of lanzar for the 20^th century, reported as 0.75 in Table 14.10 but as 0.76 in Table 14.11 and echar in the 18^th century, reported as 0.43 (see Table 14.10), while Table 14.11 displays it as 0.42. These differences arise from the fact that Van Hulle & Enghels (2024a) presumably did not use R for their calculations. The type/token ratio of echar in the 18^th century is actually 0.4250, which is rounded as 0.43 by Van Hulle & Enghels (2024a), but as 0.42 by R (see Table 14.11). This somewhat confusing rounding behaviour is explained in the help file of the round() function:

“Note that for rounding off a 5, the IEC 60559 standard (see also ‘IEEE 754’) is expected to be used, ‘go to the even digit’. Therefore round(0.5) is 0 and round(-1.5) is -2. However, this is dependent on OS services and on representation error (since e.g. 0.15 is not represented exactly, the rounding rule applies to the represented number and not to the printed number, and so round(0.15, 1) could be either 0.1 or 0.2).”

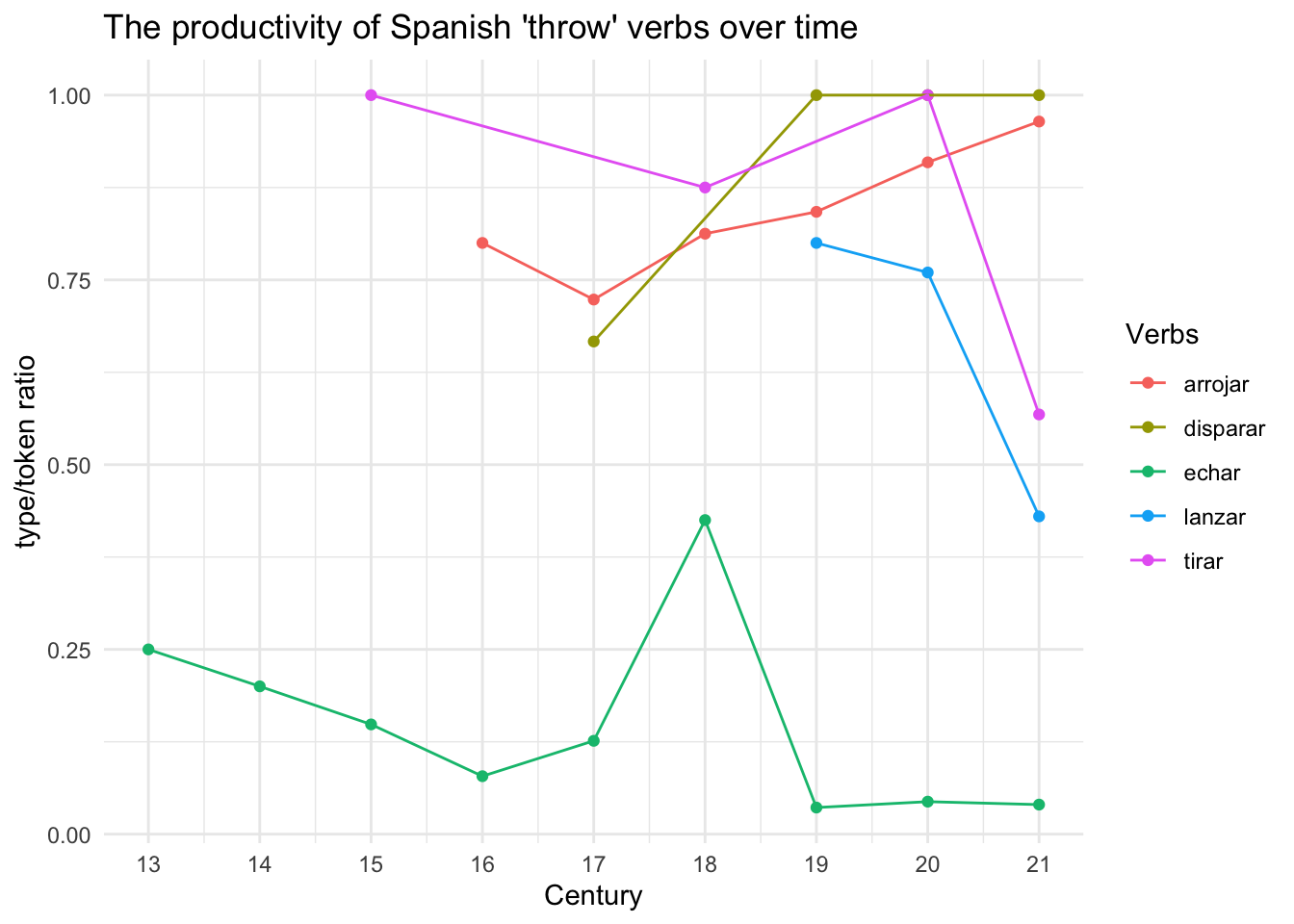
14.7.2 Visualising the type/token ratios as a line graph

For the visualisation of the type/token ratios (Figure 14.4), we create a new data frame. We start by merging the data frames verbs.investigated and verb.types using the left_join() function, ensuring that the Century and AUX variables are aligned. This results in a single data frame, which we save as type_token.

type_token <- left_join(verbs.investigated, verb.types, 
                        by = c("Century", "AUX"))

Next, we calculate the type/token ratios by adding a new column, TypeTokenRatio, to the type_token data frame using the mutate() function, which applies the type/token ratio formula to each row. Finally, we use the arrange() function to sort the data by Century and AUX organizing the results chronologically by Century and alphabetically by the verb type (AUX).

type.token.ratio <- type_token  |> 
  mutate(TypeTokenRatio = Types / n) |> 
  arrange(Century, AUX)

The output is a table with 26 rows and five columns: AUX, Century, n, and Types and TypeTokenRatio. We can display the first six rows of the table using the head() function.

head(type.token.ratio)

      AUX Century   n Types TypeTokenRatio
1   echar      13  32     8     0.25000000
2   echar      14  15     3     0.20000000
3   echar      15 101    15     0.14851485
4   tirar      15   2     2     1.00000000
5 arrojar      16  20    16     0.80000000
6   echar      16 153    12     0.07843137

Now we can use the type.token.ratio data frame with the same ggplot code that we used to create Figure 14.2 and Figure 14.3, allowing us to visualize the type/token ratios of Spanish ‘throw’ verbs over time as Figure 14.4.

ggplot(type.token.ratio, 
       aes(x = Century, 
           y = TypeTokenRatio, 
           color = AUX, 
           group = AUX)) +
  geom_point() +  # Scatterplot points
  geom_line() +   # Connect points with lines
  scale_x_continuous(breaks = 13:21) + 
  labs(title = "The productivity of Spanish 'throw' verbs over time",
       x = "Century",
       y = "type/token ratio",
       color = "Verbs") +
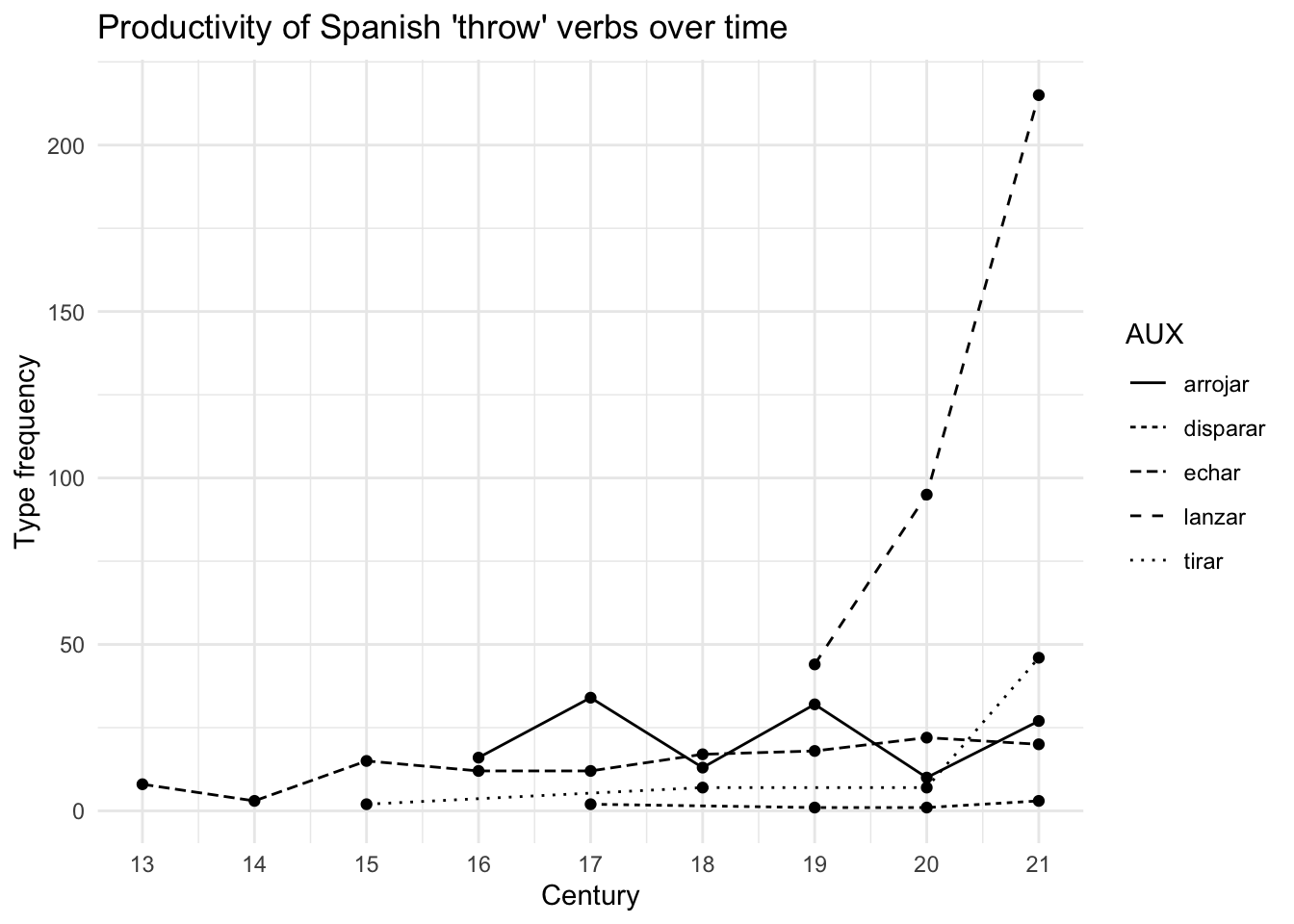
  theme_minimal()

Figure 14.4: type/token ratio of Spanish ‘throw’ Verbs Over Time

According to Van Hulle & Enghels (2024a), the verb lanzar is considered the “most productive auxiliary” due to its high type/token ratio values, despite only appearing from the 19^th century onward, and because it “was able to incorporate a more varied set of infinitives” (Van Hulle & Enghels 2024a: 228). In contrast, the type/token ratio for echar is comparably low. However, as Van Hulle & Enghels (2024a: 228) state:

“[…] the type/token ratio for the micro-construction with echar is quite stable until it considerably drops from the 19^th century on (n=0.04). This means that, although speakers used the construction more frequently, this was mainly done with a limited group of infinitives […]”

Additionally, the verbs disparar and tirar have a type/token ratio of one for the 19^th and 21^st centuries, and the 15^th and 20^th centuries, respectively. This is due to the high hapax value, i.e., “the number of types that appear only once in a text or corpus” for the respective verbs (Van Hulle & Enghels 2024a: 226). In the cases of disparar and tirar, each hapax refers to only one occurrence.

The above plot (Figure 14.4) shows more clearly that arrojar, not lanzar, is actually the most semantically productive verb. When compared with echar, as the authors of the published paper have done, lanzar does indeed appear more semantically productive. However, as Van Hulle & Enghels (2024a) note, “type/token ratio measures the realized productivity.” Based on this measure, arrojar is even more productive than lanzar, as this graphic (Figure 14.4) clearly illustrates. Van Hulle & Enghels (2024a) do not provide such a visualization, but this chapter has shown that it can aid in interpreting the realized productivity measured by the type/token ratio.

Quiz time!

Q9. What issue arises when interpreting the productivity of Spanish ‘throw’ verbs over time on the basis of Figure 14.4?

Some lines suggest a linear increase or decrease in productivity over several centuries when there were, in fact, zero occurrences of that verb in one of these centuries.
The graph incorrectly suggests that type/token ratios cannot go beyond 1.00.
The graph makes it difficult to compare the productivity of verbs across each century.
The graph incorrectly suggests that there were zero occurrences of some verbs in earlier centuries.
The graph incorrectly suggests a decrease in productivity for all verbs.

🐭 Click on the mouse for a hint.

Q10. Based on the type/token ratios displayed in Figure 14.4, which ‘throw’ verb appears to be the least productive one?

lanzar
tirar
disparar
echar
arrojar

Q11. Based on the type/token ratios displayed in Figure 14.4, which ‘throw’ verb appears to be the most productive one since the 19^th century?

arrojar
tirar
echar
lanzar
disparar

14.8 Conclusion

You have successfully completed 0 out of 11 quiz questions in this chapter.

This chapter attempted to reproduce the results of a corpus linguistics study that explores the evolution of five throw verbs in Peninsular Spanish (echar, lanzar, disparar, tirar, and arrojar) into aspectual auxiliaries in inchoative constructions that express the beginning of an event. The authors of the original study, Van Hulle & Enghels (2024a), used historical and contemporary data to analyse the development and usage of these verbs, making their research data openly accessible. As part of this chapter, we identified some discrepancies between the results we obtained on the basis of the authors’ data (Van Hulle & Enghels 2024b) and those published in the 2024 study, indicating that the version of the dataset uploaded onto TROLLing does not exactly match the one used for the published results.

We have also created some new data visualizations based on the authors’ uploaded data, which uncover patterns in the evolution of Spanish inchoative constructions that might not be immediately apparent through the examination of the tabular results alone. These visualizations underscore the effectiveness of graphical representation as a tool for understanding linguistic shifts over time—an approach not employed in the original study.

How to cite this chapter

This is a case study chapter of the web version of the textbook “Data Analysis for the Language Sciences: A very gentle introduction to statistics and data visualisation in R” by Elen Le Foll.

Please cite the current version of this chapter as:

Siahaan, Poppy. 2024. ‘Throw’ verbs in Spanish: RepRoducing the results of a corpus linguistics study. In Elen Le Foll (Ed.), Data Analysis for the Language Sciences: A very gentle introduction to statistics and data visualisation in R. Open Educational Resource. https://elenlefoll.github.io/RstatsTextbook/ (accessed DATE).

References

[1] S. T. Gries and N. C. Ellis. “Statistical Measures for Usage-Based Linguistics”. In: Language Learning 65.S1 (2015). _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1111/lang.12119, p. 228–255. ISSN: 1467-9922. DOI: 10.1111/lang.12119. https://onlinelibrary.wiley.com/doi/abs/10.1111/lang.12119.

[2] K. Pfadenhauer and E. Wiesinger, ed. Romance motion verbs in language change: Grammar, lexicon, discourse. De Gruyter, Jul. 2024. ISBN: 978-3-11-124814-1. DOI: 10.1515/9783111248141. https://www.degruyter.com/document/doi/10.1515/9783111248141/html.

[3] A. Stefanowitsch and S. Flach. “The corpus-based perspective on entrenchment”. In: Entrenchment and the psychology of language learning: How we reorganize and adapt linguistic knowledge. Ed. by H. Schmid. De Gruyter, 2017, p. 101–127. ISBN: 978-3-11-034130-0 978-3-11-034142-3. DOI: 10.1037/15969-006. https://content.apa.org/books/15969-006.

[4] S. Van Hulle and R. Enghels. Replication Data for: “The category of throw verbs as productive source of the Spanish inchoative construction. DataverseNO, V1.”. 2024. DOI: 10.18710/TR2PWJ. https://dataverse.no/dataset.xhtml?persistentId=doi:10.18710/TR2PWJ.

[5] S. Van Hulle and R. Enghels. “The category of throw verbs as productive source of the Spanish inchoative construction”. In: Romance motion verbs in language change. Ed. by K. Pfadenhauer and E. Wiesinger. De Gruyter, Jul. 2024, p. 213–240. ISBN: 978-3-11-124814-1. DOI: 10.1515/9783111248141-009. https://www.degruyter.com/document/doi/10.1515/9783111248141-009/html.

Packages used in this chapter

R version 4.4.1 (2024-06-14)
Platform: aarch64-apple-darwin20
Running under: macOS 15.1

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: Europe/Brussels
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] knitcitations_1.0.12 xfun_0.45            lubridate_1.9.3     
 [4] forcats_1.0.0        stringr_1.5.1        dplyr_1.1.4         
 [7] purrr_1.0.2          readr_2.1.5          tidyr_1.3.1         
[10] tibble_3.2.1         ggplot2_3.5.1        tidyverse_2.0.0     
[13] here_1.0.1           kableExtra_1.4.0     checkdown_0.0.12    
[16] webexercises_1.1.0  

loaded via a namespace (and not attached):
 [1] utf8_1.2.4        generics_0.1.3    xml2_1.3.6        stringi_1.8.4    
 [5] hms_1.1.3         digest_0.6.36     magrittr_2.0.3    timechange_0.3.0 
 [9] evaluate_0.24.0   grid_4.4.1        fastmap_1.2.0     plyr_1.8.9       
[13] rprojroot_2.0.4   jsonlite_1.8.8    backports_1.5.0   httr_1.4.7       
[17] fansi_1.0.6       viridisLite_0.4.2 scales_1.3.0      bibtex_0.5.1     
[21] codetools_0.2-20  cli_3.6.3         rlang_1.1.4       munsell_0.5.1    
[25] commonmark_1.9.1  withr_3.0.1       yaml_2.3.8        tools_4.4.1      
[29] tzdb_0.4.0        colorspace_2.1-0  vctrs_0.6.5       R6_2.5.1         
[33] lifecycle_1.0.4   RefManageR_1.4.0  htmlwidgets_1.6.4 pkgconfig_2.0.3  
[37] pillar_1.9.0      gtable_0.3.5      Rcpp_1.0.12       glue_1.7.0       
[41] systemfonts_1.1.0 tidyselect_1.2.1  rstudioapi_0.16.0 knitr_1.47       
[45] farver_2.1.2      htmltools_0.5.8.1 labeling_0.4.3    rmarkdown_2.27   
[49] svglite_2.1.3     compiler_4.4.1    markdown_1.13    

Package references

[1] G. Grolemund and H. Wickham. “Dates and Times Made Easy with lubridate”. In: Journal of Statistical Software 40.3 (2011), pp. 1-25. https://www.jstatsoft.org/v40/i03/.

[2] G. Moroz. checkdown: Check-Fields and Check-Boxes for rmarkdown. R package version 0.0.12. 2023. https://agricolamz.github.io/checkdown/.

[3] G. Moroz. Create check-fields and check-boxes with checkdown. 2020. https://CRAN.R-project.org/package=checkdown.

[4] K. Müller. here: A Simpler Way to Find Your Files. R package version 1.0.1. 2020. https://here.r-lib.org/.

[5] K. Müller and H. Wickham. tibble: Simple Data Frames. R package version 3.2.1. 2023. https://tibble.tidyverse.org/.

[6] R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Vienna, Austria, 2024. https://www.R-project.org/.

[7] V. Spinu, G. Grolemund, and H. Wickham. lubridate: Make Dealing with Dates a Little Easier. R package version 1.9.3. 2023. https://lubridate.tidyverse.org.

[8] H. Wickham. forcats: Tools for Working with Categorical Variables (Factors). R package version 1.0.0. 2023. https://forcats.tidyverse.org/.

[9] H. Wickham. ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York, 2016. ISBN: 978-3-319-24277-4. https://ggplot2.tidyverse.org.

[10] H. Wickham. stringr: Simple, Consistent Wrappers for Common String Operations. R package version 1.5.1. 2023. https://stringr.tidyverse.org.

[11] H. Wickham. tidyverse: Easily Install and Load the Tidyverse. R package version 2.0.0. 2023. https://tidyverse.tidyverse.org.

[12] H. Wickham, M. Averick, J. Bryan, et al. “Welcome to the tidyverse”. In: Journal of Open Source Software 4.43 (2019), p. 1686. DOI: 10.21105/joss.01686.

[13] H. Wickham, W. Chang, L. Henry, et al. ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics. R package version 3.5.1. 2024. https://ggplot2.tidyverse.org.

[14] H. Wickham, R. François, L. Henry, et al. dplyr: A Grammar of Data Manipulation. R package version 1.1.4. 2023. https://dplyr.tidyverse.org.

[15] H. Wickham and L. Henry. purrr: Functional Programming Tools. R package version 1.0.2. 2023. https://purrr.tidyverse.org/.

[16] H. Wickham, J. Hester, and J. Bryan. readr: Read Rectangular Text Data. R package version 2.1.5. 2024. https://readr.tidyverse.org.

[17] H. Wickham, D. Vaughan, and M. Girlich. tidyr: Tidy Messy Data. R package version 1.3.1. 2024. https://tidyr.tidyverse.org.

[18] Y. Xie. Dynamic Documents with R and knitr. 2nd. ISBN 978-1498716963. Boca Raton, Florida: Chapman and Hall/CRC, 2015. https://yihui.org/knitr/.

[19] Y. Xie. “knitr: A Comprehensive Tool for Reproducible Research in R”. In: Implementing Reproducible Computational Research. Ed. by V. Stodden, F. Leisch and R. D. Peng. ISBN 978-1466561595. Chapman and Hall/CRC, 2014.

[20] Y. Xie. knitr: A General-Purpose Package for Dynamic Report Generation in R. R package version 1.47. 2024. https://yihui.org/knitr/.

[21] Y. Xie. xfun: Supporting Functions for Packages Maintained by Yihui Xie. R package version 0.45. 2024. https://github.com/yihui/xfun.

[22] H. Zhu. kableExtra: Construct Complex Table with kable and Pipe Syntax. R package version 1.4.0. 2024. http://haozhu233.github.io/kableExtra/.

Gries, Stefan Th. & Nick C. Ellis. 2015. Statistical measures for usage-based linguistics. Language Learning 65(S1). 228–255. https://doi.org/10.1111/lang.12119.

Pfadenhauer, Katrin & Evelyn Wiesinger (eds.). 2024. Romance motion verbs in language change: Grammar, lexicon, discourse. De Gruyter. https://doi.org/10.1515/9783111248141.

Stefanowitsch, Anatol & Susanne Flach. 2017. The corpus-based perspective on entrenchment. In Hans-Jörg Schmid (ed.), Entrenchment and the psychology of language learning: How we reorganize and adapt linguistic knowledge, 101–127. De Gruyter. https://doi.org/10.1037/15969-006.

Van Hulle, Sven & Renata Enghels. 2024a. The category of throw verbs as productive source of the spanish inchoative construction. In Katrin Pfadenhauer & Evelyn Wiesinger (eds.), Romance motion verbs in language change, 213–240. De Gruyter. https://doi.org/10.1515/9783111248141-009.

Van Hulle, Sven & Renata Enghels. 2024b. TROLLing replication data for: “The category of throw verbs as productive source of the spanish inchoative construction. DataverseNO, V1.” https://doi.org/10.18710/TR2PWJ.

---

1. We contacted the first and corresponding author of the paper. They responded and confirmed that these discrepancies were likely due to small changes that were made to the dataset that was ultimately used in the analyses published in Van Hulle & Enghels (2024a). These changes were deemed necessary when either additional occurrences of inchoative constructions were found in the corpora, or false positives (i.e. occurrences of ‘throw’ verbs that did not enter such constructions) were later identified in the dataset. The author did not provide us with the final dataset that was used in the reported analyses.

2. The normalized frequencies of echar and lanzar are found in Table 5 (Van Hulle & Enghels 2024a: 227), whilst those for arrojar, disparar and tirar are displayed in Table 8 (Van Hulle & Enghels 2024a: 232). Note that in Tables 5 and 8 (Van Hulle & Enghels 2024a: 232) all values are rounded off to two decimal places except the normalized frequency of disparar in the 21^st which is reported as “0.0008”.

3. Note that we cannot copy the word counts directly from the paper, as the authors use the continental European format with the dot (.) as the thousand-separator and the comma (,) as a decimal point (e.g., 7.829.566 for the 13^th century). In R, however, the dot is interpreted as a decimal separator so entering 7.829.566 will generate an error:

   7.829.566

   unexpected numeric constant in "7.829.566"

4. Remember that, in base R, the notation [x, y] allows us to specify rows and columns in a data frame, where x refers to the row and y refers to the column (see Section 7.3). For example, token.data[, 1] means we are selecting all rows from the first column of token.data.